The CashValue_ME Model#

Overview#

The CashValue_ME model is a faster reimplementation of the CashValue_SE model.

The CashValue_ME model reproduces the same results as CashValue_SE, but is more suitable for processing a large number of model points. Each formula to be applied to all the model points operates on the entire set of model points at once with the help of Numpy and Pandas.

The default product specs, assumptions and input data are the same as CashValue_SE.

Changes from CashValue_SE#

Below is the list of Cells and References that are newly added or updated from CashValue_SE.

Running with 10000 model points#

The main advantage of the CashValue_ME model over the CashValue_SE model is its speed. By default, CashValue_ME is configured to run the same 4 model points as the ones in CashValue_SE, but a larger table of 10000 model points is also included in the model. The larger model point table is saved in the model folder as an Excel file named model_point_10000.xlsx, and this table is read into the model as a DataFrame named model_point_10000. The 10000 model points are all new business at time 0, and created by modifying the sample model points in basiclife.

To run the model with the larger model point table, assign the table to model_point_table:

>>> Projection.model_point_table = Projection.model_point_10000

In the code above, Projection must be defined beforehand to refer to the Projection space.

Below is the speed result of running the entire 10000 model points on a consumer PC equipped with Intel Core i5-6500T CPU and 16GB RAM.

10000 model points with CashValue_ME without split by product#
>>> timeit.timeit("Projection.result_pv()", globals=globals(), number=1)
34.3045132

>>> Projection.result_pv()
               Premiums         Death  ...  Change in AV  Net Cashflow
policy_id                              ...
1          5.349200e+07  4.852612e+05  ...  4.465141e+06  1.881696e+06
2          4.446054e+07  1.356468e+07  ...  1.604824e+07  1.177058e+07
3          1.210841e+08  7.179706e+07  ...  2.796228e+07  2.192224e+07
4          3.038400e+07  2.938897e+05  ...  4.840159e+06  4.346383e+06
5          5.989500e+07  3.342985e+05  ...  7.238519e+06  7.671440e+06
                ...           ...  ...           ...           ...
9996       2.067500e+07  5.335816e+05  ...  3.627718e+06  1.951471e+06
9997       6.690600e+07  4.291283e+05  ...  8.984202e+06  4.590207e+06
9998       7.629662e+06  4.007463e+06  ...  1.982635e+06  1.441142e+06
9999       2.835552e+06  1.258307e+06  ...  8.583928e+05  4.917449e+05
10000      1.513202e+07  3.834462e+06  ...  6.555234e+06  3.667102e+06

[10000 rows x 9 columns]

The above run projects all model points for the max length of the entire model points:

>>> Projection.max_proj_len()
1141

Since product A and B are limited term up to 20 years and C and D are whole life, it may be more efficient to run the limited term and whole life model points separately, because the limited term model points don’t need as long the length of projection period as C and D model points. You can do so by defining, for example, seg_id to filter model points in the formula of model_point(). The code below is an example of the modified formula of model_point() to filter the model points by seg_id:

>>> Projection.model_point.formula
def model_point():
    """"Target model points
    ...
    """
    cond = model_point_table_ext()['is_wl'] == (True if seg_id == 'WL' else False)
    return model_point_table_ext().loc[cond]

Assigning "WL" to seg_id results in running only whole life model points, while assigning anything other than "WL" results in running limited term model points:

>>> Projection.seg_id = 'WL'

>>> timeit.timeit("Projection.result_pv()", globals=globals(), number=1)
24.311953799999998

>>> Projection.result_pv()
               Premiums         Death  ...  Change in AV  Net Cashflow
policy_id                              ...
2          4.446054e+07  1.356468e+07  ...  1.604824e+07  1.177058e+07
3          1.210841e+08  7.179706e+07  ...  2.796228e+07  2.192224e+07
6          5.051520e+06  3.011482e+06  ...  1.152065e+06  4.933033e+04
9          5.537287e+07  3.686858e+07  ...  1.126645e+07  7.784990e+06
10         2.957650e+07  1.156441e+07  ...  9.877157e+06  6.451814e+06
                ...           ...  ...           ...           ...
9988       5.051377e+05  1.692807e+05  ...  1.715821e+05  1.065215e+05
9989       2.889266e+07  1.769398e+07  ...  5.681889e+06  4.869589e+06
9998       7.629662e+06  4.007463e+06  ...  1.982635e+06  1.441142e+06
9999       2.835552e+06  1.258307e+06  ...  8.583928e+05  4.917449e+05
10000      1.513202e+07  3.834462e+06  ...  6.555234e+06  3.667102e+06

[5015 rows x 9 columns]

>>> Projection.max_proj_len()
1141

>>> Projection.seg_id = 'NWL'

>>> timeit.timeit("Projection.result_pv()", globals=globals(), number=1)
5.201247100000003

>>> Projection.result_pv()
             Premiums          Death  ...  Change in AV  Net Cashflow
policy_id                             ...
1          53492000.0  485261.238999  ...  4.465141e+06  1.881696e+06
4          30384000.0  293889.696238  ...  4.840159e+06  4.346383e+06
5          59895000.0  334298.511514  ...  7.238519e+06  7.671440e+06
7          42066000.0  337495.895163  ...  3.513768e+06  1.355059e+06
8           5270000.0   85955.434866  ...  7.032080e+05 -2.137742e+05
              ...            ...  ...           ...           ...
9993        1116000.0    6862.126164  ...  1.498832e+05  6.988384e+04
9994       22050000.0  765048.795780  ...  3.453998e+06  3.159848e+06
9995        3420000.0   24997.118829  ...  6.067274e+05 -4.430946e+04
9996       20675000.0  533581.639585  ...  3.627718e+06  1.951471e+06
9997       66906000.0  429128.288942  ...  8.984202e+06  4.590207e+06

[4985 rows x 9 columns]

>>> Projection.max_proj_len()
1141

To keep the results for both "WL" and "NWL", you can parameterize Projection with seg_id and have Projection['WL'] and Projection['NWL'] as dynamic child spaces of Projection:

>>> Projection.parameters = ("seg_id",)

>>> Projection['WL'].model_point()
          spec_id  age_at_entry sex  ...  surr_charge_id  load_prem_rate  is_wl
policy_id                            ...
2               C            29   M  ...             NaN            0.10   True
3               D            51   F  ...          type_3            0.05   True
6               D            51   F  ...          type_3            0.05   True
9               D            59   F  ...          type_3            0.05   True
10              D            35   F  ...          type_3            0.05   True
          ...           ...  ..  ...             ...             ...    ...
9988            C            32   M  ...             NaN            0.10   True
9989            C            56   M  ...             NaN            0.10   True
9998            D            45   F  ...          type_3            0.05   True
9999            D            39   M  ...          type_3            0.05   True
10000           D            22   F  ...          type_3            0.05   True

[5015 rows x 14 columns]

>>> Projection['WL'].result_pv()
               Premiums         Death  ...  Change in AV  Net Cashflow
policy_id                              ...
2          4.446054e+07  1.356468e+07  ...  1.604824e+07  1.177058e+07
3          1.210841e+08  7.179706e+07  ...  2.796228e+07  2.192224e+07
6          5.051520e+06  3.011482e+06  ...  1.152065e+06  4.933033e+04
9          5.537287e+07  3.686858e+07  ...  1.126645e+07  7.784990e+06
10         2.957650e+07  1.156441e+07  ...  9.877157e+06  6.451814e+06
                ...           ...  ...           ...           ...
9988       5.051377e+05  1.692807e+05  ...  1.715821e+05  1.065215e+05
9989       2.889266e+07  1.769398e+07  ...  5.681889e+06  4.869589e+06
9998       7.629662e+06  4.007463e+06  ...  1.982635e+06  1.441142e+06
9999       2.835552e+06  1.258307e+06  ...  8.583928e+05  4.917449e+05
10000      1.513202e+07  3.834462e+06  ...  6.555234e+06  3.667102e+06

[5015 rows x 9 columns]

>>> Projection['NWL'].model_point()
          spec_id  age_at_entry sex  ...  surr_charge_id  load_prem_rate  is_wl
policy_id                            ...
1               B            47   M  ...          type_1             0.0  False
4               A            32   F  ...             NaN             0.1  False
5               A            28   M  ...             NaN             0.1  False
7               B            45   F  ...          type_1             0.0  False
8               B            47   F  ...          type_1             0.0  False
          ...           ...  ..  ...             ...             ...    ...
9993            B            29   M  ...          type_1             0.0  False
9994            A            52   F  ...             NaN             0.1  False
9995            B            24   M  ...          type_1             0.0  False
9996            B            47   M  ...          type_1             0.0  False
9997            B            30   M  ...          type_1             0.0  False

[4985 rows x 14 columns]

>>> Projection['NWL'].result_pv()
             Premiums          Death  ...  Change in AV  Net Cashflow
policy_id                             ...
1          53492000.0  485261.238999  ...  4.465141e+06  1.881696e+06
4          30384000.0  293889.696238  ...  4.840159e+06  4.346383e+06
5          59895000.0  334298.511514  ...  7.238519e+06  7.671440e+06
7          42066000.0  337495.895163  ...  3.513768e+06  1.355059e+06
8           5270000.0   85955.434866  ...  7.032080e+05 -2.137742e+05
              ...            ...  ...           ...           ...
9993        1116000.0    6862.126164  ...  1.498832e+05  6.988384e+04
9994       22050000.0  765048.795780  ...  3.453998e+06  3.159848e+06
9995        3420000.0   24997.118829  ...  6.067274e+05 -4.430946e+04
9996       20675000.0  533581.639585  ...  3.627718e+06  1.951471e+06
9997       66906000.0  429128.288942  ...  8.984202e+06  4.590207e+06

[4985 rows x 9 columns]

While running the entire model points at once took 34 seconds, running the whole life and limited term model points separately took about 30 seconds in total. The whole life segment is about half the size of the entire model points, and takes 24 seconds, while the entire segment takes 34 seconds, which implies the processing speed per model point improves as the number of model points gets larger.

Formula examples#

Most formulas in the CashValue_ME model are the same as those in CashValue_SE. However, some formulas are updated since they cannot be applied to vector operations without change. For example, below shows how pols_maturity, the number of maturing policies at time t, is defined differently in CashValue_SE and in CashValue_ME.

pols_maturity in CashValue_SE#
def pols_maturity(t):
    if duration_mth(t) == policy_term() * 12:
        return pols_if_at(t, "BEF_MAT")
    else:
        return 0
pols_maturity in CashValue_ME#
 def pols_maturity(t):
     return (duration_mth(t) == policy_term() * 12) * pols_if_at(t, "BEF_MAT")

In CashValue_SE, policy_term() returns an integer, such as 10 indicating a policy term of the selected model point in years, so the if clause checks if the value of duration_mth() is equal to the policy term in month:

In CashValue_SE for model point 1#
>>> policy_term()
10

>>> pols_maturity(120)
65.9357318577613

In contrast, policy_term() in CashValue_ME returns a Series of policy terms of all the model points. If the if clause were defined in the same way as in the CashValue_SE, it would result in an error, because the condition duration_mth(t) == policy_term() * 12 for a certain t returns a Series of boolean values and it is ambiguous for the Series to be in the if condition. Further more, whether the if branch or the else branch should be evaluated needs to be determined element-wise, but the if statement would not allow such element-wise branching. Instead of using the if statement, the formula in CashValue_ME achieves the element-wise conditional operation by multiplication by a Series of boolean values. In the formula in CashValue_ME, pols_if_at(t, "BEF_MAT") returns the numbers of policies at time t for all the model points as a Series. Multiplying it by (duration_mth(t) == policy_term() * 12) replaces the numbers of policies with 0 for model points whose policy terms in month are not equal to t. This operation is effectively an element-wise if operation:

In CashValue_ME at t=120#
>>> policy_term()
poind_id
1    10
2    20
3    95
4    65
dtype: int64


>>> (duration_mth(120) == policy_term() * 12)
poind_id
1     True
2    False
3    False
4    False
dtype: bool


>>> pols_maturity(120)
1    65.935732
2     0.000000
3     0.000000
4     0.000000
dtype: float64

Basic Usage#

Reading the model#

Create your copy of the savings library by following the steps on the Quick Start page. The model is saved as the folder named CashValue_ME in the copied folder.

To read the model from Spyder, right-click on the empty space in MxExplorer, and select Read Model. Click the folder icon on the dialog box and select the CashValue_ME folder.

Getting the results#

By default, the model has Cells for outputting projection results as listed in the Results section. result_cf() outputs total cashflows of all the model points, and result_pv() outputs the present values of the cashflows by model points. Both Cells outputs the results as pandas DataFrame.

By following the same steps explained in the Quick Start page using this model, You can get the results in an MxConsole and show the results as tables in MxDataViewer.

Changing the model point#

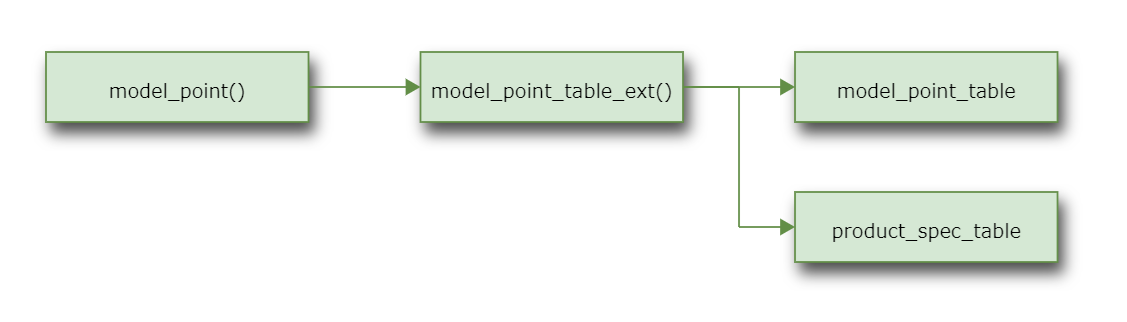
By default, model_point() returns the entire model_point_table_ext():

>>> Projection.model_point.formula
def model_point():
    return model_point_table_ext()
../../_images/diagram15.png

The calculations in Projection apply to all the model points in model_point_table. To limit the calculation target, change the model_point() formula so that model_point() returns a DataFrame that contains only the target rows. For example, to select only the model point 1:

>>> Projection.model_point.formula
def model_point():
    return model_point_table_ext().loc[1:1]

There are many methods of DataFrame for selecting its rows. See the pandas documentation for details.

When selecting only one model point, make sure that model_point() returns the model point as a DataFrame not as a Series. In the code example above, model_point_table_ext().loc[1:1] is specified instead of model_point_table_ext().loc[1], because model_point_table_ext().loc[1] would return the model point as a Series.

Also, you should be careful not to accidentally update the original DataFrame held as model_point_table.

Model Specifications#

The CashValue_ME model has only one UserSpace, named Projection, and all the Cells and References are defined in the space.

The Projection Space#

The main Space in the CashValue_ME model.

Projection is the only Space defined in the CashValue_ME model, and it contains all the logic and data used in the model.

Parameters and References

(In all the sample code below, the global variable Projection refers to the Projection Space.)

model_point_table#

All model points as a DataFrame. By default, 4 model points are defined. The DataFrame has an index named point_id.

  • spec_id

  • age_at_entry

  • sex

  • policy_term

  • policy_count

  • sum_assured

  • duration_mth

  • premium_pp

  • av_pp_init

Cells defined in Projection with the same names as these columns return the corresponding column’s values for the selected model point.

>>> Projection.model_poit_table
         spec_id  age_at_entry sex  ...  premium_pp  av_pp_init
poind_id                            ...
1              A            20   M  ...      500000           0
2              B            50   M  ...      500000           0
3              C            20   M  ...        1000           0
4              D            50   M  ...        1000           0

[4 rows x 10 columns]

The DataFrame is saved in the Excel file model_point_samples.xlsx placed in the model folder. model_point_table is created by Projection’s new_pandas method, so that the DataFrame is saved in the separate file. The DataFrame has the injected attribute of _mx_dataclident:

>>> Projection.model_point_table._mx_dataclient
<PandasData path='model_point_table_samples.xlsx' filetype='excel'>

See also

model_point_10000#

Alternative model point table

This model point table contains 10000 model points and is saved as the Excel file model_point_10000.xlsx placed in the folder. To use this table, assign it to model_point_table:

>>> Projection.model_point_table = Projection.model_point_10000
disc_rate_ann#

Annual discount rates by duration as a pandas Series.

>>> Projection.disc_rate_ann
year
0      0.00000
1      0.00555
2      0.00684
3      0.00788
4      0.00866

146    0.03025
147    0.03033
148    0.03041
149    0.03049
150    0.03056
Name: disc_rate_ann, Length: 151, dtype: float64

The Series is saved in the Excel file disc_rate_ann.xlsx placed in the model folder. disc_rate_ann is created by Projection’s new_pandas method, so that the Series is saved in the separate file. The Series has the injected attribute of _mx_dataclident:

>>> Projection.disc_rate_ann._mx_dataclient
<PandasData path='disc_rate_ann.xlsx' filetype='excel'>

See also

mort_table#

Mortality table by age and duration as a DataFrame. See basic_term_sample.xlsx included in this library for how the sample mortality rates are created.

>>> Projection.mort_table
            0         1         2         3         4         5
Age
18   0.000231  0.000254  0.000280  0.000308  0.000338  0.000372
19   0.000235  0.000259  0.000285  0.000313  0.000345  0.000379
20   0.000240  0.000264  0.000290  0.000319  0.000351  0.000386
21   0.000245  0.000269  0.000296  0.000326  0.000359  0.000394
22   0.000250  0.000275  0.000303  0.000333  0.000367  0.000403
..        ...       ...       ...       ...       ...       ...
116  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
117  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
118  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
119  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
120  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000

[103 rows x 6 columns]

The DataFrame is saved in the Excel file mort_table.xlsx placed in the model folder. mort_table is created by Projection’s new_pandas method, so that the DataFrame is saved in the separate file. The DataFrame has the injected attribute of _mx_dataclident:

>>> Projection.mort_table._mx_dataclient
<PandasData path='mort_table.xlsx' filetype='excel'>

See also

std_norm_rand#

Random numbers drawn from the standard normal distribution

A Series of random numbers drawn from the standard normal distribution indexed with scen_id and t. Used for generating investment returns. See inv_return_table().

scen_id#

Selected scenario ID

An integer indicating the selected scenario ID. scen_id is referenced in by inv_return_mth() as one of the keys to select a scenario from std_norm_rand.

surr_charge_table#

Surrender charge rates by duration

A DataFrame of multiple patterns of surrender charge rates by duration. The column labels indicate surr_charge_id(). By default, "type_1", "type_2" and "type_3" are defined.

product_spec_table#

Table of product specs

A DataFrame of product spec parameters by spec_id. model_point_table and product_spec_table columns are joined in model_point_table_ext(), and the product_spec_table columns become part of the model point attributes. The product_spec_table columns are read by the Cells with the same names as the columns:

>>> Projection.product_spec_table
        premium_type  has_surr_charge surr_charge_id  load_prem_rate  is_wl
spec_id
A             SINGLE            False            NaN            0.10  False
B             SINGLE             True         type_1            0.00  False
C              LEVEL            False            NaN            0.10   True
D              LEVEL             True         type_3            0.05   True
np#

The numpy module.

pd#

The pandas module.

Projection parameters#

This is a new business model and all model points are issued at time 0. The time step of the model is monthly. Cashflows and other time-dependent variables are indexed with t.

Cashflows and other flows that accumulate throughout a period indexed with t denotes the sums of the flows from t til t+1. Balance items indexed with t denotes the amount at t.

proj_len()

Projection length in months

max_proj_len()

The max of all projection lengths

Model point data#

The model point data is stored in an Excel file named model_point_table.xlsx under the model folder.

model_point()

Target model points

model_point_table_ext()

Extended model point table

sex()

The sex of the model points

sum_assured()

The sum assured of the model points

policy_term()

The policy term of the model points.

age(t)

The attained age at time t.

age_at_entry()

The age at entry of the model points

duration(t)

Duration of model points at t in years

duration_mth(t)

Duration of model points at t in months

has_surr_charge()

Whether surrender charge applies

is_wl()

Whether the model point is whole life

load_prem_rate()

Rate of premium loading

surr_charge_id()

ID of surrender charge pattern

premium_type()

Type of premium payment

av_pp_init()

Initial account value per policy

Assumptions#

The mortality table is stored in an Excel file named mort_table.xlsx under the model folder, and is read into mort_table as a DataFrame. mort_table_reindexed() returns a mortality table reshaped from mort_table, which is a Series indexed with Age and Duration. mort_rate() looks up mort_table_reindexed() and picks up the annual mortality rates to be applied for all the model points at time t and returns them in a Series. mort_rate_mth() converts mort_rate() to the monthly mortality rate to be applied during the month starting at time t.

../../_images/diagram24.png

The discount rate data is stored in an Excel file named disc_rate_ann.xlsx under the model folder, and is read into disc_rate_ann as a Series.

../../_images/diagram34.png

The lapse by duration is defined by a formula in lapse_rate(). expense_acq() holds the acquisition expense per policy at t=0. expense_maint() holds the maintenance expense per policy per annum. The maintenance expense inflates at a constant rate of inflation given as inflation_rate().

mort_table_last_age()

The last age of mortality tables

mort_rate(t)

Mortality rate to be applied at time t

mort_rate_mth(t)

Monthly mortality rate to be applied at time t

mort_table_reindexed()

MultiIndexed mortality table

disc_factors()

Discount factors.

disc_rate_mth()

Monthly discount rate

lapse_rate(t)

Lapse rate

expense_acq()

Acquisition expense per policy

expense_maint()

Annual maintenance expense per policy

inflation_factor(t)

The inflation factor at time t

inflation_rate()

Inflation rate

Policy values#

By default, the amount of death benefit for each policy (claim_pp()) is set equal to sum_assured.

premium_pp() is the single premium amount if the model point represents single premium policies (i.e. premium_type() is "SINGLE"), or the monthly premium amount if the model point represents level premium policies (i.e. premium_type() is "LEVEL").

claim_pp(t, kind)

Claim per policy

premium_pp(t)

Premium amount per policy

maint_fee_rate()

Maintenance fee per account value

coi_rate(t)

Cost of insurance rate per account value

surr_charge_rate(t)

Surrender charge rate

surr_charge_table_stacked()

Stacked surrender charge table

surr_charge_max_idx()

maximum index of surrender charge table

Policy decrement#

The policy decrement logic of CashValue_ME is based on that of CashValue_SE. except that each relevant formula operates on the entire model points.

pols_death(t)

Number of death

pols_if(t)

Number of policies in-force

pols_if_at(t, timing)

Number of policies in-force

pols_if_init()

Initial number of policies in-force

pols_lapse(t)

Number of lapse

pols_maturity(t)

Number of maturing policies

pols_new_biz(t)

Number of new business policies

Account Value#

The account value logic of CashValue_ME is based on CashValue_SE. except that each relevant formula operates on the entire model points.

inv_income(t)

Investment income on account value

inv_income_pp(t)

Investment income on account value per policy

inv_return_mth(t)

Rate of investment return

inv_return_table()

Table of investment return rates

av_pp_at(t, timing)

Account value per policy

net_amt_at_risk(t)

Net amount at risk per policy

coi_pp(t)

Cost of insurance charges per policy

prem_to_av_pp(t)

Per-policy premium portion put in the account value

maint_fee_pp(t)

Maintenance fee per policy

av_at(t, timing)

Account value in-force

prem_to_av(t)

Premium portion put in account value

claims_from_av(t, kind)

Account value taken out to pay claim

claims_over_av(t, kind)

Claim in excess of account value

coi(t)

Cost of insurance charges

maint_fee(t)

Maintenance fee deducted from account value

av_change(t)

Change in account value

check_av_roll_fwd()

Check account value roll-forward

Cashflows#

Cashflows are calculated as its per-policy amount times the number of policies.

The expense cashflow consists of acquisition expenses at issue and monthly maintenance expenses spent each month.

By default, commissions are defined as 5% premiums.

surr_charge(t)

Surrender charge

claims(t[, kind])

Claims

commissions(t)

Commissions

premiums(t)

Premium income

expenses(t)

Expenses

net_cf(t)

Net cashflow

Margin Analysis#

net_cf() can be expressed as the sum of expense and mortality margins. The expense margin is defined as the sum of premium loading, surrender charge and maintenance fees net of commissions and expenses. The mortality margin is defined coi() net of claims_over_av().

margin_expense(t)

Expense margin

margin_mortality(t)

Mortality margin

check_margin()

Check consistency between net cashflow and margins

Present values#

The Cells whose names start with pv_ are for calculating the present values of the cashflows indicated by the rest of their names. pv_pols_if() is not used in CashValue_SE and BasicTerm_ME.

pv_claims([kind])

Present value of claims

pv_commissions()

Present value of commissions

pv_expenses()

Present value of expenses

pv_net_cf()

Present value of net cashflows.

pv_pols_if()

Present value of policies in-force

pv_premiums()

Present value of premiums

pv_av_change()

Present value of change in account value

pv_inv_income()

Present value of investment income

check_pv_net_cf()

Check present value summation

Results#

result_cf() outputs the total cashflows of all the model points as a DataFrame:

>>> result_cf()
          Premiums         Claims      Expenses   Commissions  Net Cashflow
0     1.002000e+08  795274.520511  2.016667e+06  5.010000e+06 -1.888257e+06
1     1.982432e+05  782659.768793  1.653397e+04  9.912161e+03  1.102781e+05
2     1.965019e+05  776554.840116  1.640233e+04  9.825093e+03  1.083123e+05
3     1.947758e+05  777512.879071  1.627174e+04  9.738790e+03  1.088861e+05
4     1.930649e+05  770406.958695  1.614219e+04  9.653245e+03  1.082080e+05
           ...            ...           ...           ...           ...
1136  0.000000e+00       0.000000  0.000000e+00  0.000000e+00  0.000000e+00
1137  0.000000e+00       0.000000  0.000000e+00  0.000000e+00  0.000000e+00
1138  0.000000e+00       0.000000  0.000000e+00  0.000000e+00  0.000000e+00
1139  0.000000e+00       0.000000  0.000000e+00  0.000000e+00  0.000000e+00
1140  0.000000e+00       0.000000  0.000000e+00  0.000000e+00  0.000000e+00

[1141 rows x 5 columns]

result_pv() outputs the present values of the cashflows by model points:

>>> result_pv()
              Premiums         Death  ...  Change in AV  Net Cashflow
poind_id                              ...
1         5.000000e+07  1.350327e+05  ...  3.771029e+06  4.957050e+06
2         5.000000e+07  1.608984e+06  ...  8.740610e+06  4.241619e+06
3         2.642236e+07  6.107771e+06  ...  1.104837e+07  6.058365e+06
4         2.201418e+07  1.329419e+07  ...  4.763115e+06  2.514042e+06

[4 rows x 9 columns]

result_cf()

Result table of cashflows

result_pv()

Result table of present value of cashflows

result_pols()

Result table of policy decrement

Cells Descriptions#

proj_len()[source]#

Projection length in months

proj_len() returns how many months the projection for each model point should be carried out for all the model point. Defined as:

np.maximum(12 * policy_term() - duration_mth(0) + 1, 0)

Since this model carries out projections for all the model points simultaneously, the projections are actually carried out from 0 to max_proj_len for all the model points.

See also

max_proj_len()#

The max of all projection lengths

Defined as max(proj_len())

See also

proj_len()

model_point()[source]#

Target model points

Returns as a DataFrame the model points to be in the scope of calculation. By default, this Cells returns the entire model_point_table_ext() without change. model_point_table_ext() is the extended model point table, which extends model_point_table by joining the columns in product_spec_table. Do not directly refer to model_point_table in this formula. To select model points, change this formula so that this Cells returns a DataFrame that contains only the selected model points.

Examples

To select only the model point 1:

def model_point():
    return model_point_table_ext().loc[1:1]

To select model points whose ages at entry are 40 or greater:

def model_point():
    return model_point_table[model_point_table_ext()["age_at_entry"] >= 40]

Note that the shape of the returned DataFrame must be the same as the original DataFrame, i.e. model_point_table_ext().

When selecting only one model point, make sure the returned object is a DataFrame, not a Series, as seen in the example above where model_point_table_ext().loc[1:1] is specified instead of model_point_table_ext().loc[1].

Be careful not to accidentally change the original table held in model_point_table_ext().

See also

model_point_table_ext()[source]#

Extended model point table

Returns an extended model_point_table by joining product_spec_table on the spec_id column.

See also

sex()[source]#

The sex of the model points

Note

This cells is not used by default.

The sex column of the DataFrame returned by model_point().

sum_assured()[source]#

The sum assured of the model points

The sum_assured column of the DataFrame returned by model_point().

policy_term()[source]#

The policy term of the model points.

The policy_term column of the DataFrame returned by model_point().

age(t)[source]#

The attained age at time t.

Defined as:

age_at_entry() + duration(t)

See also

age_at_entry()[source]#

The age at entry of the model points

The age_at_entry column of the DataFrame returned by model_point().

duration(t)[source]#

Duration of model points at t in years

See also

duration_mth()

duration_mth(t)[source]#

Duration of model points at t in months

Indicates how many months the policies have been in-force at t. The initial values at time 0 are read from the duration_mth column in model_point_table through model_point(). Increments by 1 as t increments. Negative values of duration_mth() indicate future new business policies. For example, If the duration_mth() is -15 at time 0, the model point is issued at t=15.

See also

model_point()

has_surr_charge()[source]#

Whether surrender charge applies

True if surrender charge on account value applies upon lapse, False if other wise. By default, the value is read from the has_surr_charge column in model_point().

See also

is_wl()[source]#

Whether the model point is whole life

True if the model point is whole life, False if other wise. By default, the value is read from the is_wl column in model_point(). This attribute is used to determin policy_term(). If True, policy_term() is defined as mort_table_last_age() minus age_at_entry(). If False, policy_term() is read from model_point().

See also

load_prem_rate()[source]#

Rate of premium loading

This rate times premium_pp() is collected from each premium and the rest is added to the account value.

By default, the value is read from the load_prem_rate column in model_point().

See also

surr_charge_id()[source]#

ID of surrender charge pattern

A string to indicate the ID of the surrender charge pattern. The ID should be one of the column names in surr_charge_table if has_surr_charge() is True.

See also

premium_type()[source]#

Type of premium payment

Returns a string indicating the payment type, which is either "LEVEL" if level payment, or "SINGLE" if single payment.

av_pp_init()[source]#

Initial account value per policy

For existing business at time 0, returns initial per-policy accout value read from the av_pp_init column in model_point(). For new business, 0 should be entered in the column.

See also

mort_table_last_age()[source]#

The last age of mortality tables

Returns the last age whose mortality rates are all 1. If no such age is found, return the last index of the tables

See also

mort_rate(t)[source]#

Mortality rate to be applied at time t

Returns a Series of the mortality rates to be applied at time t. The index of the Series is point_id, copied from model_point().

See also

mort_rate_mth(t)[source]#

Monthly mortality rate to be applied at time t

See also

mort_table_reindexed()[source]#

MultiIndexed mortality table

Returns a Series of mortlity rates reshaped from mort_table. The returned Series is indexed by age and duration capped at 5.

disc_factors()[source]#

Discount factors.

Vector of the discount factors as a Numpy array. Used for calculating the present values of cashflows.

See also

disc_rate_mth()

disc_rate_mth()[source]#

Monthly discount rate

Nummpy array of monthly discount rates from time 0 to max_proj_len() - 1 defined as:

(1 + disc_rate_ann)**(1/12) - 1

See also

disc_rate_ann()

lapse_rate(t)[source]#

Lapse rate

By default, the lapse rate assumption is defined by duration as:

max(0.1 - 0.02 * duration(t), 0.02)

See also

duration()

expense_acq()[source]#

Acquisition expense per policy

5000 by default.

expense_maint()[source]#

Annual maintenance expense per policy

500 by default.

inflation_factor(t)[source]#

The inflation factor at time t

See also

inflation_rate()[source]#

Inflation rate

The inflation rate to be applied to the expense assumption. By defualt it is set to 0.01.

See also

claim_pp(t, kind)[source]#

Claim per policy

The claim amount per policy. The second parameter is to indicate the type of the claim, and it takes a string, which is either "DEATH", "LAPSE" or "MATURITY".

The death benefit as denoted by "DEATH", is the greater of sum_assured() and mid-month account value (av_pp_at(t, "MID_MTH")).

The surrender benefit as denoted by "LAPSE" and the maturity benefit as denoted by "MATURITY" are equal to the mid-month account value.

See also

premium_pp(t)[source]#

Premium amount per policy

Single premium amount if premium_type() is "SINGLE", monthly premium amount if premium_type() is "LEVEL".

See also

maint_fee_rate()[source]#

Maintenance fee per account value

The rate of maintenance fee on account value each month. Set to 0.01 / 12 by default.

See also

coi_rate(t)[source]#

Cost of insurance rate per account value

The cost of insuranc rate per account value per month. By default, it is set to 1.1 times the monthly mortality rate.

See also

surr_charge_rate(t)[source]#

Surrender charge rate

Surrender charge rate to be applied for lapsed policies

See also

surr_charge_table_stacked()[source]#

Stacked surrender charge table

surr_charge_table converted to a Series indexed with surrender charge ID and duration.

See also

surr_charge_max_idx()[source]#

maximum index of surrender charge table

The maximum index(duration) of surr_charge_table.

See also

pols_death(t)[source]#

Number of death

Number of policies decreased by death between t and t+1

pols_if(t)[source]#

Number of policies in-force

pols_if(t) is an alias for pols_if_at(t, "BEF_MAT").

See also

pols_if_at(t, timing)[source]#

Number of policies in-force

pols_if_at(t, timing) calculates the number of policies in-force at time t. The second parameter timing takes a string value to indicate the timing of in-force, which is either "BEF_MAT", "BEF_NB" or "BEF_DECR".

BEF_MAT

The number of policies in-force before maturity after lapse and death. At time 0, the value is read from pols_if_init(). For time > 0, defined as:

pols_if_at(t-1, "BEF_DECR") - pols_lapse(t-1) - pols_death(t-1)

BEF_NB

The number of policies in-force before new business after maturity. Defined as:

pols_if_at(t, "BEF_MAT") - pols_maturity(t)

BEF_DECR

The number of policies in-force before lapse and death after new business. Defined as:

pols_if_at(t, "BEF_NB") + pols_new_biz(t)

See also

pols_if_init()[source]#

Initial number of policies in-force

Number of in-force policies at time 0 referenced from pols_if_at(0, "BEF_MAT").

pols_lapse(t)[source]#

Number of lapse

Number of policies decreased by lapse during t and t+1.

See also

pols_maturity(t)[source]#

Number of maturing policies

The policy maturity occurs when duration_mth() equals 12 times policy_term(). The amount is equal to pols_if_at(t, "BEF_MAT").

otherwise 0.

pols_new_biz(t)[source]#

Number of new business policies

The number of new business policies. The value duration_mth(0) for the selected model point is read from the policy_count column in model_point(). If the value is 0 or negative, the model point is new business at t=0 or at t when duration_mth(t) is 0, and the pols_new_biz(t) is read from the policy_count in model_point().

See also

inv_income(t)[source]#

Investment income on account value

Investment income earned on account value during each period. For the plicies decreased by lapse and death, half the investment income is credited.

See also

inv_income_pp(t)[source]#

Investment income on account value per policy

Investment income on account value defined as:

inv_return_mth(t) * av_pp_at(t, "BEF_INV")

See also

inv_return_mth(t)[source]#

Rate of investment return

Rate of monthly investment return for scen_id and t read from inv_return_table()

See also

inv_return_table()[source]#

Table of investment return rates

Returns a Series of monthly investment retuns. The Series is indexed with scen_id and t which is inherited from std_norm_rand.

\[\exp\left(\left(\mu-\frac{\sigma^{2}}{2}\right)\Delta{t}+\sigma\sqrt{\Delta{t}}\epsilon\right)-1\]

where \(\mu=2\%\), \(\sigma=3\%\), \(\Delta{t}=\frac{1}{12}\), and \(\epsilon\) is a randome number from the standard normal distribution.

See also

av_pp_at(t, timing)[source]#

Account value per policy

av_at(t, timing) calculates the total amount of account value at time t for the policies in-force.

At each t, the events that change the account value balance occur in the following order:

  • Premium payment

  • Fee deduction

Investment income is assumed to be earned throughout each month, so at the middle of the month when death and lapse occur, half the investment income for the month is credited.

The second parameter timing takes a string to indicate the timing of the account value, which is either "BEF_PREM", "BEF_FEE", "BEF_INV" or "MID_MTH".

BEF_PREM

Account value before premium payment. At the start of the projection (i.e. when t=0), the account value is set to av_pp_init().

BEF_FEE

Account value after premium payment before fee deduction

BEF_INV

Account value after fee deduction before crediting investemnt return

MID_MTH

Account value at middle of month (t+0.5) when half the investment retun for the month is credited

See also

net_amt_at_risk(t)[source]#

Net amount at risk per policy

Return sum assured net of account value per policy.

See also

coi_pp(t)[source]#

Cost of insurance charges per policy

The cost of insurance charges per policy. Defined as the coi charge rate times net amount at risk per policy.

See also

prem_to_av_pp(t)[source]#

Per-policy premium portion put in the account value

The amount of premium per policy net of loading, which is put in the accoutn value.

See also

maint_fee_pp(t)[source]#

Maintenance fee per policy

See also

av_at(t, timing)[source]#

Account value in-force

av_at(t, timing) calculates the total amount of account value at time t for the policies represented by a model point.

At each t, the events that change the account value balance occur in the following order:

  • Maturity

  • New business and premium payment

  • Fee deduction

The second parameter timing takes a string to indicate the timing of the account value, which is either "BEF_MAT", "BEF_NB" or "BEF_FEE".

BEF_MAT

The amount of account value before maturity, defined as:

av_pp_at(t, "BEF_PREM") * pols_if_at(t, "BEF_MAT")

BEF_NB

The amount of account value before new business after maturity, defined as:

av_pp_at(t, "BEF_PREM") * pols_if_at(t, "BEF_NB")

BEF_FEE

The amount of account value before lapse and death after new business, defined as:

av_pp_at(t, "BEF_FEE") * pols_if_at(t, "BEF_DECR")

See also

prem_to_av(t)[source]#

Premium portion put in account value

The amount of premiums net of loadings, which is put in the accoutn value.

See also

claims_from_av(t, kind)[source]#

Account value taken out to pay claim

The part of the claim amount that is paid from account value. The second parameter takes a string indicating the type of the claim, which is either "DEATH", "LAPSE" or "MATURITY".

Death benefit is denoted by "DEATH", is defined as:

av_pp_at(t, "MID_MTH") * pols_death(t)

When the account value is greater than the death benefit, the death benefit equates to the account value.

Surrender benefit as denoted by "LAPSE" is defined as:

av_pp_at(t, "MID_MTH") * pols_lapse(t)

As the surrender benefit is defined as account value less surrender charge, when there is no surrender charge the surrender benefit equates to the account value.

Maturity benefit as denoted by "MATURITY" is defined as:

av_pp_at(t, "BEF_PREM") * pols_maturity(t)

By default, the maturity benefit equates to the account value of maturing policies.

See also

claims_over_av(t, kind)[source]#

Claim in excess of account value

The amount of death benefits in excess of account value. coi() net of this amount represents mortality margin.

See also

coi(t)[source]#

Cost of insurance charges

The cost of insurance charges deducted from acccount values each period.

See also

maint_fee(t)[source]#

Maintenance fee deducted from account value

See also

av_change(t)[source]#

Change in account value

Change in account value during each period, defined as:

av_at(t+1, 'BEF_MAT') - av_at(t, 'BEF_MAT')

See also

check_av_roll_fwd()[source]#

Check account value roll-forward

Returns Ture if av_at(t+1, "BEF_NB") equates to the following expression for all t, otherwise returns False:

av_at(t, "BEF_MAT")
      + prem_to_av(t)
      - maint_fee(t)
      - coi(t)
      + inv_income(t)
      - claims_from_av(t, "DEATH")
      - claims_from_av(t, "LAPSE")
      - claims_from_av(t, "MATURITY"))

See also

surr_charge(t)[source]#

Surrender charge

Surrender charge rate times account values of lapsed policies

See also

claims(t, kind=None)[source]#

Claims

The claim amount during the period from t to t+1. The optional second parameter is for indicating the type of the claim, and it takes a string, which is either "DEATH", "LAPSE" or "MATURITY", or defaults to None to indicate the total of all the types of claims during the period.

The death benefit as denoted by "DEATH" is defined as:

claim_pp(t) * pols_death(t)

The surrender benefit as denoted by "LAPSE" is defined as:

claims_from_av(t, "LAPSE") - surr_charge(t)

The maturity benefit as denoted by "MATURITY" is defined as:

claims_from_av(t, "MATURITY")

See also

commissions(t)[source]#

Commissions

By default, 100% premiums for the first year, 0 otherwise.

See also

premiums(t)[source]#

Premium income

Premium income during the period from t to t+1 defined as:

premium_pp() * pols_if_at(t, "BEF_DECR")

See also

expenses(t)[source]#

Expenses

Expenses during the period from t to t+1 defined as the sum of acquisition expenses and maintenance expenses. The acquisition expenses are modeled as expense_acq() times pols_new_biz(). The maintenance expenses are modeled as expense_maint() times inflation_factor() times pols_if_at() before decrement.

See also

net_cf(t)[source]#

Net cashflow

Net cashflow for the period from t to t+1 defined as:

premiums(t) - claims(t) - expenses(t) - commissions(t)

See also

margin_expense(t)[source]#

Expense margin

Expense margin is defined as the sum of premium loading, surrender charge and maintenance fees net of commissions and expenses.

The sum of the expense margin and mortality margin add up to the net cashflow.

See also

margin_mortality(t)[source]#

Mortality margin

Mortality margin is defined coi() net of claims_over_av().

The sum of the expense margin and mortality margin add up to the net cashflow.

See also

check_margin()[source]#

Check consistency between net cashflow and margins

Returns True if net_cf() equates to the sum of margin_expense() and margin_mortality() for all t, otherwise, returns False.

See also

pv_claims(kind=None)[source]#

Present value of claims

See claims() for the parameter kind.

See also

pv_commissions()[source]#

Present value of commissions

See also

pv_expenses()[source]#

Present value of expenses

See also

pv_net_cf()[source]#

Present value of net cashflows.

Defined as:

pv_premiums() + pv_inv_income()
- pv_claims() - pv_expenses() - pv_commissions() - pv_av_change()

See also

pv_pols_if()[source]#

Present value of policies in-force

Note

This cells is not used by default.

The discounted sum of the number of in-force policies at each month. It is used as the annuity factor for calculating net_premium_pp().

pv_premiums()[source]#

Present value of premiums

See also

pv_av_change()[source]#

Present value of change in account value

See also

pv_inv_income()[source]#

Present value of investment income

The discounted sum of monthly investment income.

See also

check_pv_net_cf()[source]#

Check present value summation

Check if the present value of net_cf() matches the sum of the present values of each cashflow. Returns the check result as True or False.

result_cf()[source]#

Result table of cashflows

See also

result_pv()[source]#

Result table of present value of cashflows

See also

result_pols()[source]#

Result table of policy decrement

See also

On this page
Show Source