The BasicTermASL_ME Model#

Overview#

The BasicTermASL_ME is an adjustable step length(ASL) model, and projects the cashflows of in-force policies at time 0 and future new business policies issued after time 0. As is the case with BasicTerm_ME, time-dependent cells in BasicTermASL_ME carry out calculations for all model points, and returns values for all the model points as pandas Series or numpy array objects.

Unlike BasicTerm_ME, with BasicTermASL_ME the user can specify the length of each projection step, from 1 month to 1 year. By default, the first 60 steps are monthly projections, while steps after that are annual. This model reads issue date information from model point input, and handles policy anniversaries precisely.

Space Inheritance#

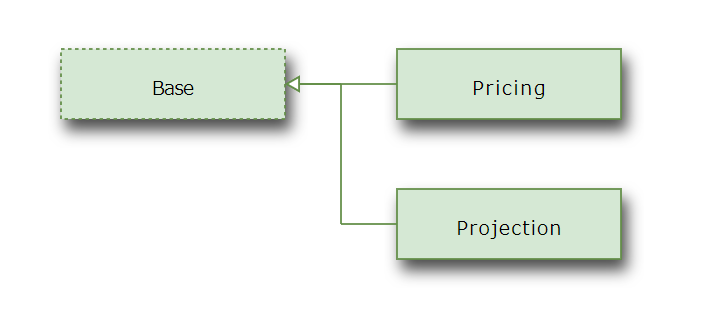
BasicTermASL_ME has 3 spaces, namely Base, Projection and Pricing. Base is the base space of Projection and and Pricing, and most Cells and References are defined in Base. Pricing is for calculating premiums. In Pricing, the issue dates of all model points are set to the projection start date in model_point(). premium_pp() calculates premiums per 1000 sum assured per payment from loading_prem() and the present values of claims over present value of polices in-force for premium payments. Pricing.premium_pp() is brought in to Projection as pricing_premium_pp and referenced by Projection.premium_pp().

../../_images/diagram1.png

Projection Steps#

Projection steps are indexed with i. Step i starts from one day after date_(i) and ends on date_(i+1). date_(0) is the projection start date. The start date is specified by a date string assigned to date_init. date_(i) returns a Timestamp object. The length of each projection step can be specified by offset() cells. offset(i) should return the length of step i as a pandas DateOffset object, so that the object can be added to the Timestamp values of date_(i). date_(i) should always be an end-of-month date, so offset(i) should return DateOffset objects such that date_(i) are always end-of-month dates. YearEnd and MonthEnd objects are good examples. By default, ‘2021-12-31’ is set to date_init, and the first 60 steps are monthly and steps after that are annual.

>>> BasicTermASL_ME.Base.date_(0)
Timestamp('2021-12-31 00:00:00')

>>> BasicTermASL_ME.Base.date_(60)
Timestamp('2026-12-31 00:00:00')

>>> BasicTermASL_ME.Base.date_(61)
Timestamp('2027-12-31 00:00:00')

>>> BasicTermASL_ME.Base.offset(0)
<MonthEnd>

>>> BasicTermASL_ME.Base.offset(60)
<YearEnd: month=12>

Policy Anniversary#

When a policy’s anniversary date is in a projection step, some cells, such as pols_lapse() and premiums() calculate their values by separately calculating the parts before and after the anniversary and then adding them up. For example, the formula of pols_lapse() looks like below:

def pols_lapse(i, j=None):

    if j is None:
        return pols_lapse(i, 'LAST') + pols_lapse(i, 'NEXT')

    elif j == 'LAST':
        lapse = 1 - (1 - lapse_rate(i))**(last_part(i) / 12)
        return (pols_if_at(i, "BEG_STEP") - pols_death(i, 'LAST')) * lapse

    elif j == 'NEXT':
        lapse = 1 - (1 - lapse_rate(i+1))**(next_part(i) / 12)
        return (pols_if_at(i, "AFT_NB") - pols_death(i, 'NEXT')) * lapse

    else:
        raise ValueError('invalid j')

When the second parameter j is not given, pols_lapse(i) adds pols_lapse(i, 'LAST') and pols_lapse(i, 'NEXT') and returns the their sum. pols_lapse(i, 'LAST') returns the number of lapsed policies before the policy anniversary in Step i. pols_lapse(i, 'NEXT') returns the number of lapsed policies during Step i after the policy anniversary in Step i. If the length of Step i is shorter than a full year, then there may not be an anniversary date in Step i, in which case pols_lapse(i, 'LAST') should be the entire pols_lapse(i) and pols_lapse(i, 'NEXT') should be zero.

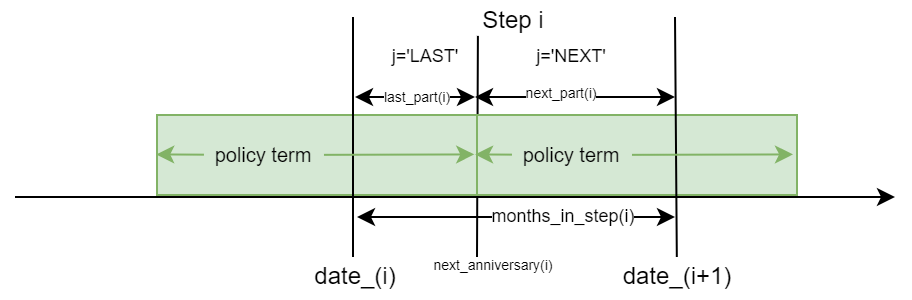
The figure below illustrates adjacent policy terms and the policy anniversary between them occurring during Step i. next_anniversary(i) returns the first anniversary date after date_(i) for all model points as a Series of Timestamp objects. months_in_step(i) returns the number of months in Step i as an integer.

last_part(i) returns the length of time from date_(i) to next_anniversary(i) in months. next_part(i) returns the length of time from next_anniversary(i) to date_(i+1) in months. The fractional portions of last_part(i) and next_part(i) represent residual days.

../../_images/policy_anniversary.png

Model Specifications#

The Base space#

The sole base Space in the BasicTermASL_ME model.

Base is the only base Space defined in the BasicTermASL_ME model, and it contains logic and data commonly used in the sub spaces of Base.

Parameters and References

(In all the sample code below, the global variable Projection refers to the Projection Space.)

model_point_table#

All model points as a DataFrame. The sample model point data was generated by generate_model_points_ASL.ipynb included in the library. By default, model_point() returns this entire model_point_table. The DataFrame has an index named point_id, and has the following columns:

  • age_at_entry

  • sex

  • policy_term

  • policy_count

  • sum_assured

  • issue_date

  • payment_freq

  • payment_term

Cells with the same names as these columns return the corresponding columns.

The DataFrame is saved in the Excel file model_point_table.xlsx located in the model folder. model_point_table is created by Projection’s new_pandas method, so that the DataFrame is saved in the separate file.

See also

disc_rate_ann#

Annual discount rates by duration as a pandas Series.

>>> Projection.disc_rate_ann
year
0      0.00000
1      0.00555
2      0.00684
3      0.00788
4      0.00866

146    0.03025
147    0.03033
148    0.03041
149    0.03049
150    0.03056
Name: disc_rate_ann, Length: 151, dtype: float64

The Series is saved in the Excel file disc_rate_ann.xlsx placed in the model folder. disc_rate_ann is created by Projection’s new_pandas method, so that the Series is saved in the separate file.

See also

mort_table#

Mortality table by age and duration as a DataFrame. See basic_term_sample.xlsx included in this library for how the sample mortality rates are created.

>>> Projection.mort_table
            0         1         2         3         4         5
Age
18   0.000231  0.000254  0.000280  0.000308  0.000338  0.000372
19   0.000235  0.000259  0.000285  0.000313  0.000345  0.000379
20   0.000240  0.000264  0.000290  0.000319  0.000351  0.000386
21   0.000245  0.000269  0.000296  0.000326  0.000359  0.000394
22   0.000250  0.000275  0.000303  0.000333  0.000367  0.000403
..        ...       ...       ...       ...       ...       ...
116  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
117  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
118  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
119  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
120  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000

[103 rows x 6 columns]

The DataFrame is saved in the Excel file mort_table.xlsx placed in the model folder. mort_table is created by Projection’s new_pandas method, so that the DataFrame is saved in the separate file.

See also

date_init#

The projection start date as a string in the YYYY-MM-DD format. The start date needs to be an end-of-month date. By default, ‘2021-12-31’ is assigned.

np#

The numpy module.

pd#

The pandas module.

Projection parameters#

date_(i)

Date at each projection step.

months_(i)

Number of elapsed months

months_in_step(i)

Returns the number of months in step i

step_to_month(i)

Returns the number of months for step i

max_proj_len()

The upper bound for the time index i

month_to_step(m)

Returns step index for months

offset(i)

Time interval in step i

Model point data#

age(i)

The attained age at date_(i).

age_at_entry()

The age at entry of the model points

issue_date()

Issue ages of the model points

model_point()

Target model points

duration_m(i)

Duration of model points at i in months

duration_y(i)

Duration of model points at period i in years

sex()

The sex of the model points

sum_assured()

The sum assured of the model points

policy_term()

The policy term of the model points.

payment_freq()

Payment frequency

payment_lag(i, j)

Average timing of premium payments.

payment_term()

Premium payment period in years

Assumptions#

mort_rate(i)

Mortality rate to be applied at time t

mort_table_reindexed()

MultiIndexed mortality table

expense_acq()

Acquisition expense per policy

expense_maint()

Annual maintenance expense per policy

inflation_factor(i)

The inflation factor for Period i.

inflation_rate()

Inflation rate

lapse_rate(i)

Lapse rate

proj_len()

Projection length in months

disc_factors()

Discount factors.

disc_factors_prem(j)

Discount factors for premiums.

disc_rate(i)

Discount rate for period i

Policy attributes#

claim_pp(i)

Claim per policy

loading_prem()

Loading per premium

premium_pp()

Premium per policy

is_active(i)

Indicates if model points are active.

is_paying(i)

Indicates if premiums are being paid

is_maturing(i)

Indicates if model points are maturing in step i.

last_part(i[, freq_id])

Length of time till next anniversary in step i

next_part(i)

Lentgh of time after next anniversary

next_anniversary(i[, freq_id])

Nex anniversary dates

net_premium_rate()

Net premium per policy

pay_count(i[, j])

Number of premium payments in step i

Policy decrement#

pols_death(i[, j])

Number of death

pols_if(i)

Number of policies in-force

pols_if_at(i, timing)

Number of policies in-force

pols_if_avg(i)

Average number of policies in-force in step i

pols_if_init()

Initial number of policies in-force

pols_lapse(i[, j])

Number of lapse in step i

pols_maturity(i)

Number of maturing policies

pols_new_biz(i)

Number of new business policies

pols_if_pay(i, j)

Number of policies in-force for premium payment

Cashflows#

premiums(i[, j])

Premium income

claims(i)

Claims

commissions(i)

Commissions

expenses(i)

Expenses

net_cf(i)

Net cashflow

Present values#

pv_claims()

Present value of claims

pv_commissions()

Present value of commissions

pv_expenses()

Present value of expenses

pv_net_cf()

Present value of net cashflows.

pv_pols_if()

Present value of policies in-force

pv_pols_if_pay()

Present value of polices in-force for premium payments

pv_premiums()

Present value of premiums

Results#

result_cells(name[, point_id, j])

Output values of a given cells

result_cf()

Result table of cashflows

result_pols()

Result table of policy decrement

result_pv()

Result table of present value of cashflows

Validation#

check_pay_count()

Check pay_count().

The Pricing space#

Space to calculate premiums

This space is for calculating premiums. To calculate premiums, model_point() adjusts the issue ages read from model_point_table so that all the model points become new business issued the day after date_(0).

model_point()

Target model points

premium_pp()

Premium per policy

net_premium_rate()

Net premium 1000 sum assured.

The Projection space#

Space to carry out cashflow projections

This space is for carrying out cashflow projections. The only difference from its base space, Base is that Pricing.premium_pp is assigned to pricing_premium_pp in this space, and premium_pp() is overridden to reference pricing_premium_pp and returns the values of it.

pricing_premium_pp#

Pricing.premium_pp

premium_pp()

Premium per policy

Cells Descriptions#

date_(i)[source]#

Date at each projection step.

Returns a date representing each projection step as pandas Timestamp. date_(0) is read from date_init. For i > 0, date_(i) is defined recursively as:

date_(i-1) + offset(i-1)

date_(i) must always return an end-of-month date. The length of each projection step is specified by offset(). Items indexed with i and representing the change of a quantity in a projection period such as cashflows, represents the change during the projection period starting from one day after date_(i) and ending on date_(i+1)

See also

months_(i)[source]#

Number of elapsed months

Returns the number of elapsed months from date_(0) at date_(i).

months_in_step(i)[source]#

Returns the number of months in step i

Returns the number of month between date_(i) and date_(i+1).

step_to_month(i)[source]#

Returns the number of months for step i

Return the number of months from date_(0) to date_(i).

See also

max_proj_len()[source]#

The upper bound for the time index i

Defined as:

month_to_step(max(proj_len()))

Note that proj_len() retuns lengths in months while this cells retuns an index value converted by month_to_step().

month_to_step(m)[source]#

Returns step index for months

For a given number of months elapsed from date_(0), returns the minimum step index such that step_to_month(i) is equal to or greater than m.

offset(i)[source]#

Time interval in step i

This cells if for controlling the number of months in step i. Step i is from one day after date_(i) to date_(i+1). This cells should return an object of a sub calass of pandas DateOffset, such as MonthEnd and YearEnd object. The returned object must always represent end of month, and must not be longer than 1 year.

To set the length of step i to N monthhs, offset(i) should return pd.offsets.MonthEnd(N). To set the length to 1 year, offset(i) should return pd.offsets.Year(1).

By default, the formula is set so that the model projects monthly for the first 60 months (5 years) then annually after that.

offset() is defined as:

if i < 60:
    return pd.offsets.MonthEnd(1)
else:
    return pd.offsets.YearEnd(1)

See also

age(i)[source]#

The attained age at date_(i).

Defined as:

age_at_entry() + duration_y(i)

See also

age_at_entry()[source]#

The age at entry of the model points

The age_at_entry column of the DataFrame returned by model_point().

issue_date()[source]#

Issue ages of the model points

The issue_age column of the DataFrame returned by model_point().

model_point()[source]#

Target model points

Returns as a DataFrame the model points to be in the scope of calculation. By default, this Cells returns the entire model_point_table without change. To select model points, change this formula so that this Cells returns a DataFrame that contains only the selected model points.

Examples

To select only the model point 1:

def model_point():
    return model_point_table.loc[1:1]

To select model points whose ages at entry are 40 or greater:

def model_point():
    return model_point_table[model_point_table["age_at_entry"] >= 40]

Note that the shape of the returned DataFrame must be the same as the original DataFrame, i.e. model_point_table.

When selecting only one model point, make sure the returned object is a DataFrame, not a Series, as seen in the example above where model_point_table.loc[1:1] is specified instead of model_point_table.loc[1].

Be careful not to accidentally change the original table.

duration_m(i)[source]#

Duration of model points at i in months

Returns durations at period i in months of all model points as a Series indexed with model point ID. duration_m(i) is calculated from date_(i) and issue_date(). duration_m() is 0 in the issue month.

Negative values of duration_m() indicate future new business policies. For example, If the duration_m() is -15 at time 0, the model point is issued 15 months later.

See also

duration_y(i)[source]#

Duration of model points at period i in years

Returns a Series calculated as:

duration_m(i) // 12

See also

duration_m()

sex()[source]#

The sex of the model points

Note

This cells is not used by default.

The sex column of the DataFrame returned by model_point().

sum_assured()[source]#

The sum assured of the model points

The sum_assured column of the DataFrame returned by model_point().

policy_term()[source]#

The policy term of the model points.

The policy_term column of the DataFrame returned by model_point().

payment_freq()[source]#

Payment frequency

The payment_freq column of the DataFrame returned by model_point(), which indicates the number of payments in a year of each model point.

payment_lag(i, j)[source]#

Average timing of premium payments.

If ‘LAST’ is passed to j, returns the average time in months from date_(i) to a payment before the next policy anniversary. Defined as:

last_part(i, freq_id='PREM') + max(pay_count(i, 'LAST') - 1, 0) * pay_interval / 2

where pay_interval is defined as 12 // payment_freq().

If ‘NEXT’ is passed to j, returns the average time in months from the next anniversary date to a premium payment after the policy anniversary. Defined as:

max(pay_count(i, 'NEXT') - 1, 0) * pay_interval / 2

See also

payment_term()[source]#

Premium payment period in years

The payment_term column of the DataFrame returned by model_point().

mort_rate(i)[source]#

Mortality rate to be applied at time t

Returns a Series of the mortality rates to be applied at time t. The index of the Series is point_id, copied from model_point().

See also

mort_table_reindexed()[source]#

MultiIndexed mortality table

Returns a Series of mortlity rates reshaped from mort_table. The returned Series is indexed by age and duration capped at 5.

expense_acq()[source]#

Acquisition expense per policy

300 by default.

expense_maint()[source]#

Annual maintenance expense per policy

60 by default.

inflation_factor(i)[source]#

The inflation factor for Period i.

Defined as:

(1 + inflation_rate())**(months_in_step(i)/12)

See also

inflation_rate()[source]#

Inflation rate

0.01 by default

lapse_rate(i)[source]#

Lapse rate

By default, the lapse rate assumption is defined by duration as:

max(0.1 - 0.02 * duration_y(i), 0.02)

See also

duration_y()

proj_len()[source]#

Projection length in months

proj_len() returns how many months the projection for each model point should be carried out for all the model point. Defined as:

np.maximum(12 * policy_term() - duration_m(0) + 1, 0)

Since this model carries out projections for all the model points simultaneously, the projections are actually carried out from 0 to max_proj_len for all the model points.

See also

disc_factors()[source]#

Discount factors.

Vector of the discount factors as a Numpy array. Used for calculating the present values of cashflows.

See also

disc_factors_prem(j)[source]#

Discount factors for premiums.

Returns a 2D numpy array. The array contains discount factors for discounting premiums of each model point. The timings of premium cashflows are adjusted by payment_lag(). Since payment_lag() differs by model point, disc_factors_prem() returns a 2D array by model point and by time index i. In each projection step, premium payments before and after policy anniversary are modeled separately, so different discount factors are returned depending of the value of j. When j='LAST', the returned discount factors are for discounting premiums paid before policy anniversary, while when j='NEXT', the factors are for premiums after the anniversary. For each i and j, disc_factors_prem() is defined as:

(1 + disc_rate(i))**(-t)

where t is defined as for j='LAST':

(months_(i) + payment_lag(i, j)) / 12

and for j='NEXT' as:

(months_(i) + last_part(i, j) + payment_lag(i, j)) / 12
Parameters:

j – ‘LAST’ or ‘NEXT’

See also

disc_rate(i)[source]#

Discount rate for period i

Returns an annual discount rate to be applied for period i, which starts one day after date_(i) and ends on date_(i+1). The discount rate is read from disc_rate_ann. If the number of years elapsed from date_init changes during the period, discount rates read from disc_rate_ann are prorated.

See also

claim_pp(i)[source]#

Claim per policy

The claim amount per plicy. Defaults to sum_assured().

loading_prem()[source]#

Loading per premium

0.5 by default. Used by premium_pp() in the Pricing space.

See also

premium_pp()[source]#

Premium per policy

This cells is defined in sub spaces.

is_active(i)[source]#

Indicates if model points are active.

Returns a Series indexed with model point ID indicating whether each model point is active at date_(i) by True or False. A model point is active if it has been issued but not expired. is_active() is defined as:

(0 <= duration_m(i)) & (duration_m(i) < policy_term() * 12)

See also

is_paying(i)[source]#

Indicates if premiums are being paid

Returns a Series of booleans indexed with model point ID indicating whether each model point is paying premiums at date_(i). Defined as:

is_active(i) & (duration_m(i) < payment_term() * 12)

See also

is_maturing(i)[source]#

Indicates if model points are maturing in step i.

Returns a Series indexed with model point ID indicating whether each model point is maturing during the period from one day after date_(i) to date_(i+1) by True or False. is_maturing() is defined as:

(duration_m(i) < policy_term() * 12) & (policy_term() * 12 <= duration_m(i+1))

See also

last_part(i, freq_id='ANV')[source]#

Length of time till next anniversary in step i

When freq_id takes its default value ‘ANV’, last_part() returns and a Series indexed with model point ID that indicates for each model point the length of time in months until the next policy anniversary in step i. The decimal fraction of the length, if any, represents the proportion of the number of days befor anniversary in the anniversary months. The measured part corresponds to the remaining policy year the model point is in at date_(i). If no policy anniversary is in Step i, then months_in_step(i) is returned. If ‘PREM’ is given to freq_id, the lengh of time in months till the next payment date is returned.

See also

next_part(i)[source]#

Lentgh of time after next anniversary

Returns the length of time in month after the next anniversary during the step i. If no anniversary is in step i, then months_in_step(i) is returned.

Defined as:

months_in_step(i) - last_part(i)

See also

next_anniversary(i, freq_id='ANV')[source]#

Nex anniversary dates

Returns a Series of the next anniversary dates for all the model points.

When the second parameter freq_id is ommitted or takes the default value of ‘ANV’, the next anniversary date for each model point is calculated as the first policy anniversary date that comes after date_(i).

When freq_id is ‘PREM’, returns the next payment date after date_(i), based on the premium payment cycle calculated from payment_freq() and issue_date().

See also

net_premium_rate()[source]#

Net premium per policy

Note

This cells is implmented in the Pricing subspace.

pay_count(i, j=None)[source]#

Number of premium payments in step i

The number of premium payments in step i (from 1 day after date_(i) to date_(i+1)). If ‘LAST’ is passed to j, only the payments in step i during the last policy period (the year that the policy is in at date_(i)) is counted. If ‘NEXT’ is passed to j, only the payments in step i after the next policy anniversary is counted.

Parameters:

  • i – Step index

  • j (optional) – None (default), ‘LAST’ or ‘NEXT’

See also

pols_death(i, j=None)[source]#

Number of death

The number of death during step i.

pols_if(i)[source]#

Number of policies in-force

pols_if(t) is an alias for pols_if_at(t, 'BEG_STEP').

See also

pols_if_at(i, timing)[source]#

Number of policies in-force

pols_if_at(t, timing) calculates and returns the number of policies in-force at various timings in step i. The second parameter timing takes a string value to indicate the timing, which is either 'BEG_STEP', 'DECR_LAST', 'AFT_MAT', 'AFT_NB' or 'DECR_NEXT'.

BEG_STEP

The number of policies in-force at the beginning of step i. At time 0, the value is read from pols_if_init(). For time > 0, it is equal to pols_if_at(i-1, 'DECR_NEXT').

DECR_LAST

The number of policies in-force reflecting decrement by lapse and death before the next policy anniversary in step i. Defined as:

pols_if_at(i, 'BEG_STEP') - pols_lapse(i, 'LAST') - pols_death(i, 'LAST')

AFT_MAT

The number of policies after reflecting maturity decrement. Defined as:

pols_if_at(i, 'DECR_LAST') - pols_maturity(i)

AFT_NB

The number of policies after reflecting increase by new business. Defined as:

pols_if_at(i, 'AFT_MAT') + pols_new_biz(i)

DECR_NEXT

The number of policies after reflecting decrement by lapse and death after the next policy anniversary in step i. Defined as:

pols_if_at(i, 'AFT_NB') - pols_lapse(i, 'NEXT') - pols_death(i, 'NEXT')

See also

pols_if_avg(i)[source]#

Average number of policies in-force in step i

For policies existing on date_(i+1), defined as the mean of pols_if_at(i, 'BEG_STEP') and pols_if_at(i+1, 'BEG_STEP').

For policies maturing during step i, defined as the mean of pols_if_at(i, 'BEG_STEP') and pols_if_at(i, 'DECR_LAST').

pols_if_init()[source]#

Initial number of policies in-force

Number of in-force policies at time 0 referenced from pols_if_at(0, 'BEF_MAT').

pols_lapse(i, j=None)[source]#

Number of lapse in step i

By default, returns a Series each of whose elements represents the number of policies lapsed during step i for each model point. If ‘LAST’ is passed to j, only lapse before the next anniversary in step i is counted. If ‘NEXT’ is passed to j, only lapse after the next anniversary is counted.

Parameters:

  • i – Step index

  • j (optional) – None, ‘LAST’ or ‘NEXT’

See also

pols_maturity(i)[source]#

Number of maturing policies

Returns a Series each of whose elements represent the number of policies maturing in step i for a model point. Maturity occurs when duration_m() equals 12 times policy_term(). The amount is equal to pols_if_at(t, "DECR_LAST").

Otherwise 0.

See also

pols_new_biz(i)[source]#

Number of new business policies

Returns a Series each of whose elements represents the number of new business policies issued in step i. Policies are issued when the following condition is met:

(duration_m(i) < 0) & (duration_m(i+1) >= 0)

The numbers of new business policies are read from the policy_count column in model_point().

See also

pols_if_pay(i, j)[source]#

Number of policies in-force for premium payment

Returns a Series each of whose elements represents the number of policies in-force adjusted for payment_lag(). If ‘LAST’ is passed to j, returns the number of in-force policies at payment_lag(i, 'LAST') months past date_(i).

If ‘NEXT’ is passed to j, returns the number of in-force policies at payment_lag(i, 'NEXT') months past next_anniversary(i).

See also

premiums(i, j=None)[source]#

Premium income

By default, returns a Series each of whose elements represent premium income of a model point in step i. If ‘LAST’ is passed to j, only premiums before the next anniversary in step i are aggregated. If ‘NEXT’ is passed to j, only premiums after the next anniversary are aggregated.

See also

claims(i)[source]#

Claims

Claims incurred during the period from date_(i) + 1 to date_(i+1) defined as:

claim_pp(i) * pols_death(i)

See also

commissions(i)[source]#

Commissions

By default, 100% premiums for the first policy year, 0 otherwise.

See also

expenses(i)[source]#

Expenses

Expenses for Period i. defined as the sum of acquisition expenses and maintenance expenses. The acquisition expenses are modeled as expense_acq() times pols_new_biz(). The maintenance expenses are modeled as expense_maint() times inflation_factor() times pols_if_avg().

See also

net_cf(i)[source]#

Net cashflow

Net cashflow during step i defined as:

premiums(i) - claims(i) - expenses(i) - commissions(i)

See also

pv_claims()[source]#

Present value of claims

Returns a Numpy array of the presenet values of claims.

See also

pv_commissions()[source]#

Present value of commissions

Returns a Numpy array of the presenet values of commissions.

See also

pv_expenses()[source]#

Present value of expenses

Returns a Numpy array of the presenet values of expenses.

See also

pv_net_cf()[source]#

Present value of net cashflows.

Defined as:

pv_premiums() - pv_claims() - pv_expenses() - pv_commissions()

See also

pv_pols_if()[source]#

Present value of policies in-force

Note

This cells is not used by default.

pv_pols_if_pay()[source]#

Present value of polices in-force for premium payments

Calculated for ‘LAST’ and ‘NEXT’ separately, as pay_count() times pols_if_pay() discounted by disc_factors_prem().

See also

pv_premiums()[source]#

Present value of premiums

Returns a Numpy array of the presenet values of premiums.

See also

result_cells(name, point_id=None, j=None)[source]#

Output values of a given cells

Returns as a DataFrame the values of a cells specified by name for all i. By default, returns the values for all model points. If point_id is specified, returns the values only of the model point. If ‘LAST’ or ‘NEXT’ is passed to j, only the values of the ‘LAST’ or ‘NEXT’ part of name are aggregated.

result_cf()[source]#

Result table of cashflows

See also

result_pols()[source]#

Result table of policy decrement

See also

result_pv()[source]#

Result table of present value of cashflows

See also

check_pay_count()[source]#

Check pay_count().

Return True if, for all model points, the sum of the numbers of past and future premium payments equates to payment_term() times payment_freq(). Th numbers of future payments are calculated by summing pay_count() for all i from 0 to max_proj_len() - 1. The numbers of past payments are calculated from duration_m(0), payment_freq() and payment_term().

See also

model_point()[source]#

Target model points

model_point() adjusts the issue date colum of the DataFrame read from model_point_table for the pricing purpose. For all model points, the issue dates are set to the date one day after date_(0).

premium_pp()[source]#

Premium per policy

Returns a Series of premiums per policy per payment for all model points, defined as:

(1 + loading_prem()) * (sum_assured() / 1000) * net_premium_rate()

See also

net_premium_rate()[source]#

Net premium 1000 sum assured.

Calculates and returns a Series of net premium rates per 1000 sum assured per payment for all model points. Defined as:

(1000 / sum_assured()) * pv_claims() / pv_pols_if_pay()

See also

  • sum_assured()

  • pv_claims()

  • pv_pols_if_pay()

premium_pp()[source]#

Premium per policy

A Series of premium per policy for all the model points. Defined as pricing_premium_pp(), which is premium_pp in Pricing space.