The BasicTerm_SE Model

Overview

The BasicTerm_SE model is a variation of BasicTerm_S, and it projects the cashslows of in-force policies at time 0 and future new business policies issued at or after time 0.

While BasicTerm_S is a new business model and it assumes all model points are issued at time 0, BasicTerm_SE reads the duration of each model point at time 0 from the model point file. The duration of a model point being N months (N > 0) means N months have elapsed before time 0 since the issue of the model point. If the duration is -N months, the model point is issued N months after time 0. Premium rates are fed into the model from a table which is assigned to premium_table. The rates are calculated by BasicTerm_M. How to create the table is demonstrated in the create_premium_table.ipynb notebook included in this library.

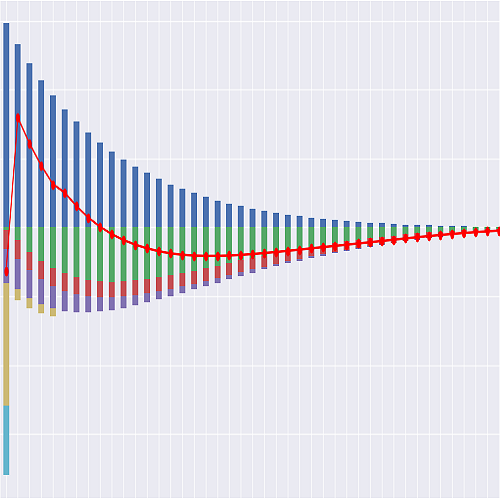
Other specifications of BasicTerm_SE are the same as BasicTerm_S. The model is a monthly step model and projects insurance cashflows of a sample model point at a time. The modeled product is a level-premium plain term product with no surrender value. The projected cashflows are premiums, claims, expenses and commissions. The assumptions used are mortality rates, lapse rates, discount rates, expense, inflation and commission rates. The present values of the cashflows are also calculated. The premium amount for each individual model point is calculated as the net premium with loadings, where the net premium is calculated from the present value of the claims.

Changes from BasicTerm_S

Below is the list of Cells and References that are newly added or updated from BasicTerm_S.

• model_point_table

• premium_table <new>

• duration()

• duration_mth() <new>

• expenses()

• pols_death()

• pols_if()

• pols_if_at() <new>

• pols_if_init()

• pols_lapse()

• pols_maturity()

• pols_new_biz() <new>

• premiums()

• premium_pp()

• proj_len()

• result_pols() <new>

The number of policies at a certain time can take different values depending on the timing of policy inflows and outflows at the same time. To represent different values for the number of policies depending on the timing of the policy flows, pols_if_at(t, timing) is introduced. pols_if_at(t, timing) calculates the number of policies in-force at time t and has a parameter named timing in addition to t. Strings are passed to timing to indicate at what timing the number of polices in-force is measured.

• "BEF_DECR": Before lapse and death

• "BEF_MAT": Before maturity

• "BEF_NB": Before new business

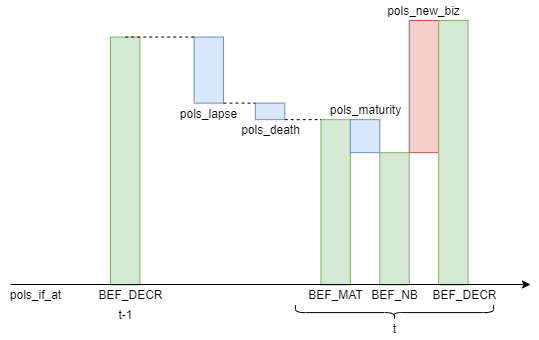
The figure below illustrates how various policy inflows and outflows are modeled in this model for one calculation step from time t-1 to time t.

pols_lapse(t) and pols_death(t) are the number of lapse and death from t-1 to t. It is assumed that policies mature at the beginning of each month, and new business policies enter at the beginning of the month but after the maturity in that month.

model_point_table has the duration_mth column, and the column is read into the duration_mth(0). If duration_mth(0) is positive, the model point is in-force policies and the number of policies at time 0 is read from the policy_count column in model_point_table into pols_if_init(), and pols_if_at(0, "BEF_MAT") is set from pols_if_init(). duration_mth() increments by 1 each step. If duration_mth() is negative, policy_count is read into pols_new_biz() when duration_mth() becomes 0.

Since projections for in-force policies do not start from their issuance, the premium rates are calculated externaly by BasicTerm_M and fed into the model as a table. The premium rates are stored in premium_table.xlsx in the model folder and read into premium_table as a Series.

Basic Usage

Reading the model

Create your copy of the basiclife library by following the steps on the Quick Start page. The model is saved as the folder named BasicTerm_SE in the copied folder.

To read the model from Spyder, right-click on the empty space in MxExplorer, and select Read Model. Click the folder icon on the dialog box and select the BasicTerm_SE folder.

Getting the results

By default, the model has Cells for outputting projection results as listed in the Results section. result_cf() outputs cashflows of the selected model point, result_pv() outputs the present values of the cashflows, result_pols() outputs the decrement table of the model point. All the Cells outputs the results as pandas DataFrame.

See the Quick Start page for how to get the results in an MxConsole and view the results in MxDataViewer.

Changing the model point

The model point to be selected is determined by point_id in Projection. It is 1 by default. model_point_table contains all the 10,000 sample model points as a pandas DataFrame. To change the model point to another one, set the other model point’s ID to point_id. Setting the new point_id clears all the values of Cells that are specific to the previous model point.

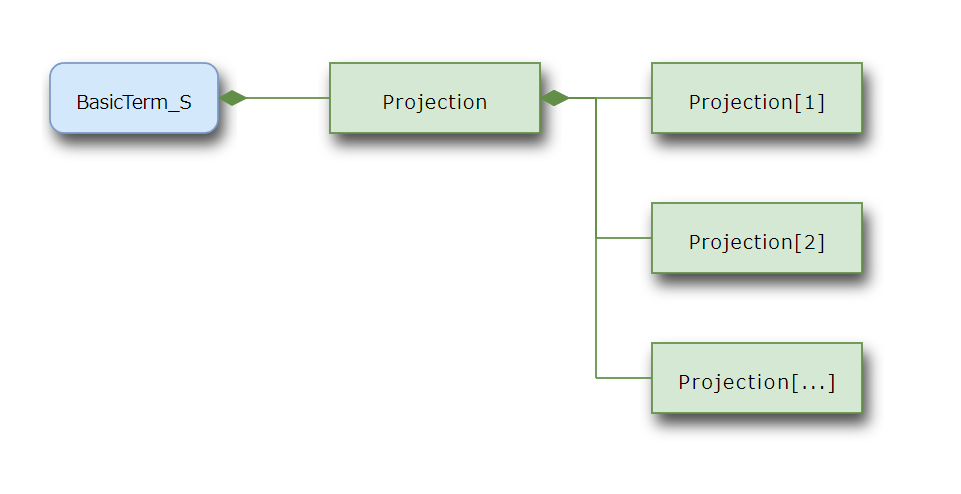
Getting multiple results

The Projection space is parameterized with point_id, i.e. the Projection space can have dynamic child spaces, such as Projection[1], Projection[2], Projection[3] …, each of which represents the Projection for each of the model points.

Note

Getting results for too many dynamic child spaces takes a considerable amount of time. The default BasicTerm_SE model would take more than a minute for 1000 model points on an ordinary spec PC. To calculate for many model points, consider using the BasicTerm_ME model.

Model Specifications

The BasicTerm_SE model has only one UserSpace, named Projection, and all the Cells and References are defined in the space.

The Projection Space

The main Space in the BasicTerm_SE model.

Projection is the only Space defined in the BasicTerm_SE model, and it contains all the logic and data used in the model.

Parameters and References

(In all the sample code below, the global variable Projection refers to the Projection Space.)

point_id

The ID of the selected model point. point_id is defined as a Reference, and its value is used for determining the selected model point. By default, 1 is assigned. To select another model point, assign its model point ID to it:

>>> Projection.point_id = 2

point_id is also defined as the parameter of the Projection Space, which makes it possible to create dynamic child space for multiple model points:

>>> Projection.parameters
('point_id',)

>>> Projection[1]
<ItemSpace BasicTerm_SE.Projection[1]>

>>> Projection[2]
<ItemSpace BasicTerm_SE.Projection[2]>

See also

• model_point_table

• model_point()

model_point_table

All model points as a DataFrame. The sample model point data was generated by generate_model_points_with_duration.ipynb included in the library. The DataFrame has an index named point_id, and model_point() returns a record as a Series whose index value matches point_id. The DataFrame has the following columns:

• age_at_entry

• sex

• policy_term

• policy_count

• sum_assured

• duration_mth

Cells defined in Projection with the same names as these columns return the corresponding column’s values for the selected model point.

>>> Projection.model_poit_table
           age_at_entry sex  ...  sum_assured  duration_mth
policy_id                    ...
1                    47   M  ...       622000             1
2                    29   M  ...       752000           210
3                    51   F  ...       799000            15
4                    32   F  ...       422000           125
5                    28   M  ...       605000            55
                ...  ..  ...          ...           ...
9996                 47   M  ...       827000           157
9997                 30   M  ...       826000           168
9998                 45   F  ...       783000           146
9999                 39   M  ...       302000            11
10000                22   F  ...       576000           166

[10000 rows x 6 columns]

The DataFrame is saved in the Excel file model_point_table.xlsx placed in the model folder. model_point_table is created by Projection’s new_pandas method, so that the DataFrame is saved in the separate file. The DataFrame has the injected attribute of _mx_dataclident:

>>> Projection.model_point_table._mx_dataclient
<PandasData path='model_point_table.xlsx' filetype='excel'>

See also

• point_id

• model_point()

• age_at_entry()

• sex()

• policy_term()

• pols_if_init()

• sum_assured()

• duration_mth()

premium_table

Premium rate table by entry age and duration as a Series. The table is created using BasicTerm_M as demonstrated in create_premium_table.ipynb. The table is stored in premium_table.xlsx in the model folder.

>>> Projection.premium_table
age_at_entry  policy_term
20            10             0.000046
              15             0.000052
              20             0.000057
21            10             0.000048
              15             0.000054
                               ...
58            15             0.000433
              20             0.000557
59            10             0.000362
              15             0.000471
              20             0.000609
Name: premium_rate, Length: 120, dtype: float64

disc_rate_ann

Annual discount rates by duration as a pandas Series.

>>> Projection.disc_rate_ann
year
0      0.00000
1      0.00555
2      0.00684
3      0.00788
4      0.00866

146    0.03025
147    0.03033
148    0.03041
149    0.03049
150    0.03056
Name: disc_rate_ann, Length: 151, dtype: float64

The Series is saved in the Excel file disc_rate_ann.xlsx placed in the model folder. disc_rate_ann is created by Projection’s new_pandas method, so that the Series is saved in the separate file. The Series has the injected attribute of _mx_dataclident:

>>> Projection.disc_rate_ann._mx_dataclient
<PandasData path='disc_rate_ann.xlsx' filetype='excel'>

See also

• disc_rate_mth()

• disc_factors()

mort_table

Mortality table by age and duration as a DataFrame. See basic_term_sample.xlsx included in this library for how the sample mortality rates are created.

>>> Projection.mort_table
            0         1         2         3         4         5
Age
18   0.000231  0.000254  0.000280  0.000308  0.000338  0.000372
19   0.000235  0.000259  0.000285  0.000313  0.000345  0.000379
20   0.000240  0.000264  0.000290  0.000319  0.000351  0.000386
21   0.000245  0.000269  0.000296  0.000326  0.000359  0.000394
22   0.000250  0.000275  0.000303  0.000333  0.000367  0.000403
..        ...       ...       ...       ...       ...       ...
116  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
117  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
118  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
119  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000
120  1.000000  1.000000  1.000000  1.000000  1.000000  1.000000

[103 rows x 6 columns]

The DataFrame is saved in the Excel file mort_table.xlsx placed in the model folder. mort_table is created by Projection’s new_pandas method, so that the DataFrame is saved in the separate file. The DataFrame has the injected attribute of _mx_dataclident:

>>> Projection.mort_table._mx_dataclient
<PandasData path='mort_table.xlsx' filetype='excel'>

See also

• mort_rate()

• mort_rate_mth()

np

The numpy module.

pd

The pandas module.

Projection parameters

The time step of the model is monthly. Cashflows and other time-dependent variables are indexed with t.

Projection is carried out separately for individual model points. proj_len() calculates the number of months to be projected for the selected model point.

Cashflows and other flows that accumulate throughout a period indexed with t denote the sums of the flows from t til t+1. Balance items indexed with t denote the amount at t.

proj_len()

Projection length in months

Model point data

The model point data is stored in an Excel file named model_point_table.xlsx under the model folder.

model_point()	The selected model point as a Series
sex()	The sex of the selected model point
sum_assured()	The sum assured of the selected model point
policy_term()	The policy term of the selected model point.
age(t)	The attained age at time t.
age_at_entry()	The age at entry of the selected model point
duration(t)	Duration of the selected model point at t in years
duration_mth(t)	Duration of the selected model point at t in months

Assumptions

The mortality table is stored in an Excel file named mort_table.xlsx under the model folder, and is read into mort_table as a DataFrame. mort_rate() looks up mort_table and picks up the annual mortality rate to be applied for the selected model point at time t. mort_rate_mth() converts mort_rate() to the monthly mortality rate to be applied during the month starting at time t.

The discount rate data is stored in an Excel file named disc_rate_ann.xlsx under the model folder, and is read into disc_rate_ann as a Series.

The lapse by duration is defined by a formula in lapse_rate(). expense_acq() holds the acquisition expense per policy at t=0. expense_maint() holds the maintenance expense per policy per annum. The maintenance expense inflates at a constant rate of inflation given as inflation_rate().

mort_rate(t)	Mortality rate to be applied at time t
mort_rate_mth(t)	Monthly mortality rate to be applied at time t
disc_factors()	Discount factors.
disc_rate_mth()	Monthly discount rate
lapse_rate(t)	Lapse rate
expense_acq()	Acquisition expense per policy
expense_maint()	Annual maintenance expense per policy
inflation_factor(t)	The inflation factor at time t
inflation_rate()	Inflation rate

Policy values

By default, the amount of death benefit for each policy (claim_pp()) is set equal to sum_assured.

The payment method is monthly whole term payment for all model points. The monthly premium per policy (premium_pp()) is calculated for each policy as sum_assured() times the premium rate in premium_table. for age_at_entry() and policy_term() of the policy. net_premium_pp() and loading_prem() are not used in BasicTerm_SE and BasicTerm_ME.

This product is assumed to have no surrender value.

claim_pp(t)	Claim per policy
net_premium_pp()	Net premium per policy
loading_prem()	Loading per premium
premium_pp()	Monthly premium per policy

Policy decrement

At t=0

If the selected model point represents in-force policies, i.e. the duration_mth of the model point in model_point_table is positive, pols_if_at(0, "BEF_MAT") is set to the value through pols_if_init().

At each projection step

pols_if_at(t, timing) represents the number of policies at t. The timing parameter can take the following string values.

• "BEF_MAT": Before maturity

• "BEF_NB": Before new business

• "BEF_DECR": Before lapse and death

Policy flows and in-force at each timing from t-1 to t are calculated recursively as follows:

• pols_if_at(t-1, "BEF_DECR") is calculated by adding pols_new_biz(t-1) to pols_if_at(t-1, "BEF_NB").

• pols_if_at(t, "BEF_MAT") is calculated by deducting pols_lapse(t) and pols_death(t) from pols_if_at(t-1, "BEF_DECR").

• pols_if_at(t, "BEF_NB") is calculated by deducting pols_maturity(t) from pols_if_at(t, "BEF_MAT").

• pols_if_at(t, "BEF_DECR") is calculated by pols_new_biz(t) from pols_if_at(t, "BEF_NB").

It is assumed that policies mature at the beginning of each month, and new business policies enter at the beginning of the month but after the maturity in that month. pols_if(t) is an alias for pols_if_at(t, "BEF_MAT").

The figure below illustrates how various policy inflows and outflows are modeled in this model for one calculation step from time t-1 to time t.

pols_death(t)	Number of death occurring at time t
pols_if(t)	Number of policies in-force
pols_if_at(t, timing)	Number of policies in-force
pols_if_init()	Initial number of policies in-force
pols_lapse(t)	Number of lapse occurring at time t
pols_maturity(t)	Number of maturing policies
pols_new_biz(t)	Number of new business policies

Cashflows

An acquisition expense at t=0 and maintenance expenses thereafter comprise expense cashflows.

Commissions are assumed to be paid out during the first policy year and the commission amount is assumed to be 100% premium during the first year and 0 afterwards.

claims(t)	Claims
commissions(t)	Commissions
premiums(t)	Premium income
expenses(t)	Expenses
net_cf(t)	Net cashflow

Present values

The Cells whose names start with pv_ are for calculating the present values of the cashflows indicated by the rest of their names. pv_pols_if() is not used in BasicTerm_SE and BasicTerm_ME.

pv_claims()	Present value of claims
pv_commissions()	Present value of commissions
pv_expenses()	Present value of expenses
pv_net_cf()	Present value of net cashflows.
pv_pols_if()	Present value of policies in-force
pv_premiums()	Present value of premiums
check_pv_net_cf()	Check present value summation

Results

result_cf() outputs the cashflows of the selected model point as a DataFrame:

>>> result_cf()
        Premiums       Claims    Expenses  Commissions  Net Cashflow
0    8156.240000  2939.548223  430.000000  8156.240000  -3369.548223
1    8084.493113  2913.690299  426.217477  8084.493113  -3339.907776
2    8013.377352  2888.059836  422.468228  8013.377352  -3310.528064
3    7942.887165  2862.654832  418.751959  7942.887165  -3281.406792
4    7873.017050  2837.473306  415.068381  7873.017050  -3252.541687
..           ...          ...         ...          ...           ...
115  5416.841591  5512.481202  312.332343     0.000000   -407.971953
116  5406.889171  5502.353062  311.758491     0.000000   -407.222382
117  5396.955036  5492.243531  311.185694     0.000000   -406.474188
118  5387.039154  5482.152574  310.613949     0.000000   -405.727369
119     0.000000     0.000000    0.000000     0.000000      0.000000

result_pv() outputs the present values of the cashflows and also their percentages against the present value of premiums as a DataFrame:

>>> result_pv()
         Premiums         Claims      Expenses   Commissions   Net Cashflow
PV  708379.130574  474803.297001  38902.884356  85874.887301  108798.061916

result_cf()	Result table of cashflows
result_pv()	Result table of present value of cashflows
result_pols()	Result table of policy decrement