Smith & Wilson algorithm#
Smith & Wilson is a widely used algorithm that can do both interpolation and extrapolation of rates at the same time. This implementation is based on the Technical documentation of the _Methodology to derive EIOPA’s risk-free interest rate term structure (Version published on 12/09/2019).
This example#
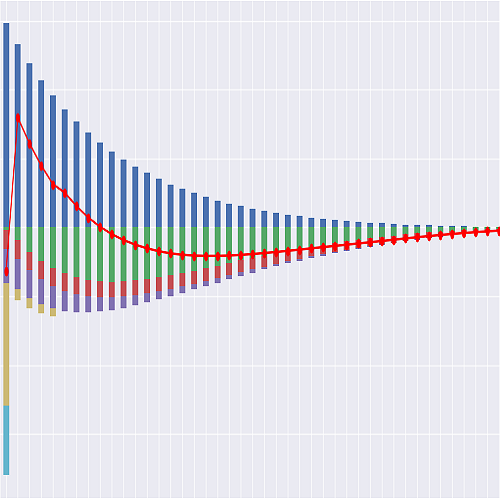
The example is taken from EIOPA’s own Excel implementation tool (Smith-Wilson Risk-Free Interest Rate Extrapolation Tool 27102015.xlsb). In this example we have observed the zero-cupon bond rates for bonds maturing in 1 year, 2 years, … 20 years. We are interested in extrapolating the curve for up to 65 years. To make the code more readable, numpy is used for matrix multiplication.
[1]:
import numpy as np
from smith_wilson_funcs import SWCalibrate, SWExtrapolate
Inputs#
Observed spot rates (r_Obs)
Maturities for the observed spot rates (M_Obs)
Ultimate Forward Rate (ufr)
Convergence parameter alpha (alpha)
Targeted maturities (M_Target)
[2]:
M_Obs = np.transpose(np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]))
r_Obs = np.transpose(np.array([0.0131074591432979, 0.0222629098372424, 0.0273403667327403, 0.0317884414257146, 0.0327205345299401, 0.0332867589595655, 0.0336112121443886, 0.0341947663149128, 0.0345165922380981, 0.0346854377006694, 0.0357173340791270, 0.0368501673784445, 0.0376263620230677, 0.0385237084707761, 0.0395043823351044, 0.0401574909803133, 0.0405715278625131, 0.0415574765441695, 0.0415582458410996, 0.0425511326946310]))
ufr = 0.042 # Ultimate froward rate ufr represents the rate to which the rate curve will converge as time increases.
alpha = 0.142068; # Convergence speed parameter alpha controls the speed at which the curve converges towards the ufr from the last liquid point.
M_Target = np.transpose(np.arange(1,66)) # For which maturities do we want the SW algorithm to calculate the rates. In this case, for every year up to 65.
Implementation#
[3]:
b = SWCalibrate(r_Obs,M_Obs, ufr, alpha) # The calibration of the kernel functions
# is done by the function Calibrate_b.
r_Target = SWExtrapolate(M_Target,M_Obs, b, ufr, alpha) # The interpolation/extrapolation of targeted
# maturitites is done by the function ExtrapolateSW.
print("The interpolated/extrapolated rates are:")
print(r_Target)
The interpolated/extrapolated rates are:
[0.01310746 0.02226291 0.02734037 0.03178844 0.03272053 0.03328676
0.03361121 0.03419477 0.03451659 0.03468544 0.03571733 0.03685017
0.03762636 0.03852371 0.03950438 0.04015749 0.04057153 0.04155748
0.04155825 0.04255113 0.04366562 0.04455613 0.04526287 0.04581885
0.04625123 0.04658238 0.04683074 0.04701152 0.04713727 0.04721831
0.04726318 0.04727891 0.04727127 0.04724504 0.04720411 0.04715169
0.04709043 0.04702247 0.04694957 0.04687315 0.04679439 0.04671421
0.04663338 0.0465525 0.04647204 0.0463924 0.04631385 0.04623664
0.04616092 0.04608682 0.04601443 0.04594381 0.04587498 0.04580797
0.04574276 0.04567935 0.0456177 0.0455578 0.04549959 0.04544304
0.0453881 0.04533473 0.04528288 0.0452325 0.04518354]
Test#
The vector “expected” contains the values from the Excel implementation released by EIOPA. This is not needed for the actual calculations but is used at the end to show the goodness of fit at the end. The second norm of the difference between the Excel results and Matlab implementation is shown below.
[4]:
expected = np.transpose(np.array([ 0.0131074591433162, 0.0222629098372631, 0.0273403667327665, 0.0317884414257348, 0.0327205345299595, 0.0332867589595818, 0.0336112121444057, 0.0341947663149282, 0.0345165922381123, 0.0346854377006820, 0.0357173340791390, 0.0368501673784565, 0.0376263620230795, 0.0385237084707877, 0.0395043823351151, 0.0401574909803222, 0.0405715278625236, 0.0415574765441811, 0.0415582458411092, 0.0425511326946399, 0.0436656239235407, 0.0445561338093701, 0.0452628707713729, 0.0458188495571263, 0.0462512293260686, 0.0465823804152550, 0.0468307431055235, 0.0470115242330582, 0.0471372655651476, 0.0472183095640757, 0.0472631822720417, 0.0472789087725782, 0.0472712735066854, 0.0472450353102873, 0.0472041051721557, 0.0471516932406448, 0.0470904304327322, 0.0470224690500156, 0.0469495660338741, 0.0468731518591676, 0.0467943875455887, 0.0467142118366739, 0.0466333802421182, 0.0465524973460913, 0.0464720435419177, 0.0463923971530968, 0.0463138527348181, 0.0462366362129754, 0.0461609174043216, 0.0460868203676226, 0.0460144319580649, 0.0459438088931750, 0.0458749835854031, 0.0458079689527213, 0.0457427623823397, 0.0456793489926264, 0.0456177043135153, 0.0455577964851157, 0.0454995880572642, 0.0454430374586101, 0.0453881001922050, 0.0453347298048383, 0.0452828786693675, 0.0452324986125916, 0.0451835414157220]))
print(np.linalg.norm(r_Target-expected, ord=2))
4.884045506039511e-14